Nyní jste na stránce, která vysvětluje nejdůležitější pojmy. Pokud chcete na popis vztahů, nebo příklad využijte následující odkazy.

Soustava soustava souřadnic – Pojmy

Abyste se seznámili se soustavou souřadnic, měli byste znát následující pojmy:

soustava souřadnic, osa soustavy souřadnic ( osa x, osa y), počátek, souřadnicový zápis,

kartézská soustava souřadnic, polární soustava souřadnic, zeměpisná soustava souřadnic, 

Wikipedia: Soustava souřadnic.

Dále budeme mluvit pouze o Kartézské soustavě souřadnic. ( Slovo kartézská je podle Descarta, jehož jméno se latinsky píše Cartesius).

Soustava souřadnic

Jednorozměrná soustava souřadnic

Nejjednodužší soustavou souřadnic je číselná osa

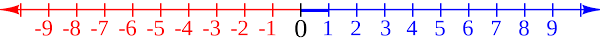
Pomocí číselné osy určujeme polohu bodu na přímce. Jde vlastně o jednorozměrnou soustavu souřadnic. Je to naprosto běžná soustava souřadnic. Podívejte se na svoje pravítko, metr, nebo pásmo. Ty jsou reprezentanty jednorozměrné číselné osy. Sice jen její kladné části, ale jako příklad to stačí.

Běžně se setkáváme s dvourozměrnou nebo třírozměrnou soustavou souřadnic.

Dvourozměrná soustava souřadnic

V kartézské souřadnice jsou to dvě přímky (číselné osy) , které jsou na sebe kolmé. Obě číselné osy mají stejné vzdálenosti mezi body. To proto, aby vznikla pravoúhlá čtvercová síť. Dvourozměrná soustava souřadnic představuje rovinu, plochu. V reálném životě třeba podlahu.

Kartézskou soustavu souřadnic v rovině označujeme Oxy.

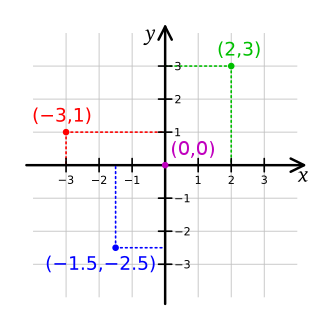
Bod (0,0) je v průniku číselných os. Říkáme mu počátek.

Kvadranty – bude vysvětleno později.

Souřadnicový zápis

Bod (2,3) je bod jehož souřadnice jsou 2 – na ose x, 3 – na ose y. Kdybychom bod nazvali např B. Tak bychom napsali B=[2,3]. Této formě zápisu říkáme souřadnicový zápis.

Ostatní body mají následující souřadnicový zápis:

A= [-3,1]

C=[-1.5;-2.5]

Trojrozměrná soustava souřadnic

Když k dvourozměrné soustavě souřadnic přidáme třetí rozměr, vznikne (kupodivu) trojrozměrná soustava souřadnic. Třetí rozměr – třetí souřadná osa – je kolmý na předchozí dvě osy. Když vezmeme jako příklad podlahu, tak třetí rozměr určuje výšku, v jaké se určitý předmět nachází nad (nebo pod) podlahou.

Roviny určené dvojicemi souřadnicových os se nazývají souřadnicové roviny. Osy x,y určují jednu souřadnicovou rovinu. Osy x, z určují druhou souřadnicovou rovinu a osy y,z určují třetí souřadnicovou rovinu.

Kartézskou soustavu souřadnic v prostoru označujeme Oxyz.

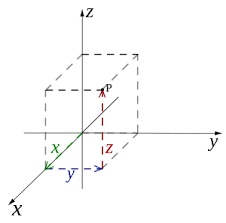
Oktanty – bude vysvětleno později.

Souřadnicový zápis

Protože popisujeme trojrozměrný prostor, musíme použít 3 souřadnice. Standardně se zapisuje následovně: D=[1;2;5 ] tj. bod D má souřadnice x=1; y=2; z=5.

Odkazy

Moc hezky je v soustava souřadnic v rozsahu základní školy vysvětlena zde:

Khanova škola na YouTube: